Exemplo De Grafico Quando O Limite Existe E Vale Zero – Exemplo De Gráfico Quando O Limite Existe E Vale Zero é um conceito fundamental no cálculo que descreve o comportamento de uma função à medida que a entrada se aproxima de um determinado valor. Quando um limite existe e vale zero, significa que a função se aproxima de zero à medida que a entrada se aproxima do ponto em questão.
Essa situação é frequentemente encontrada em aplicações práticas, como o estudo do movimento de objetos, o crescimento de populações e o comportamento de sistemas dinâmicos.
Este artigo explorará o conceito de limite zero através da análise de diferentes tipos de gráficos que representam funções com esse comportamento. Investigaremos as características visuais desses gráficos, destacando como o limite zero é visualizado e como ele se relaciona com o comportamento da função.
Além disso, apresentaremos exemplos práticos de como o limite zero é aplicado em diversas áreas, como física, engenharia e economia.
Exemplo de Gráfico Quando o Limite Existe e Vale Zero: Exemplo De Grafico Quando O Limite Existe E Vale Zero
Neste artigo, exploraremos o conceito de limite em matemática, com foco específico em situações onde o limite existe e vale zero. Abordaremos a representação gráfica de tais limites, analisando diferentes tipos de gráficos e suas características visuais. Além disso, discutiremos exemplos práticos de aplicações do limite zero em diversos campos.
Introdução
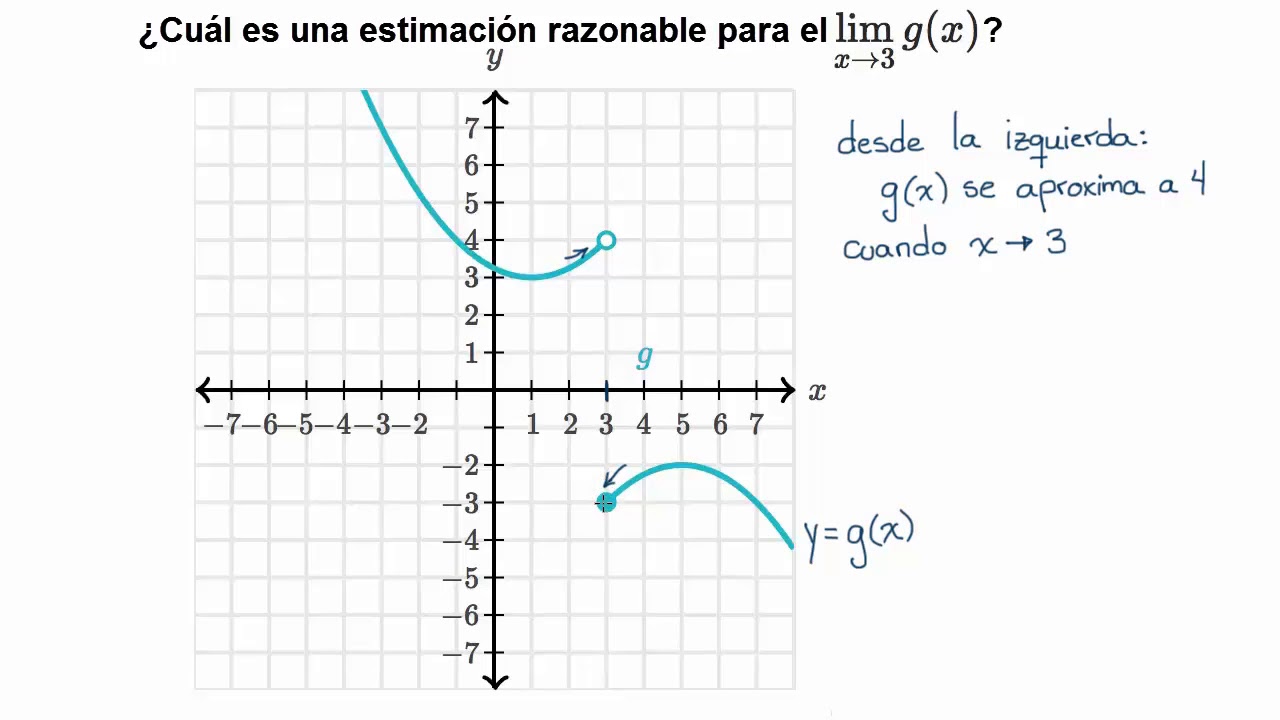
Em matemática, o conceito de limite é fundamental para o estudo do comportamento de funções. O limite de uma função em um determinado ponto representa o valor a que a função se aproxima quando a variável independente se aproxima desse ponto.
Em outras palavras, o limite indica o comportamento da função “próximo” a um determinado ponto.
Quando o limite de uma função em um ponto existe e vale zero, significa que a função se aproxima de zero à medida que a variável independente se aproxima desse ponto. Isso pode ser interpretado como a função “tendendo” a zero nesse ponto.
Existem diversos exemplos práticos de situações onde um limite existe e vale zero. Por exemplo, a função f(x) = 1/x tem limite zero quando x tende ao infinito. Isso significa que, à medida que x aumenta indefinidamente, o valor de f(x) se aproxima cada vez mais de zero.
Outro exemplo é a função f(x) = x^2 – 1, que tem limite zero quando x tende a 1. Isso significa que, à medida que x se aproxima de 1, o valor de f(x) se aproxima cada vez mais de zero.
Tipos de Gráficos
Vários tipos de gráficos podem ser utilizados para representar funções com limites que existem e valem zero. Cada tipo de gráfico possui suas características visuais específicas que permitem visualizar o limite zero de forma diferente. A seguir, apresentamos uma tabela com diferentes tipos de gráficos e suas características:
| Tipo de Gráfico | Características Visuais |
|---|---|
| Gráfico de Linhas | A linha do gráfico se aproxima do eixo x à medida que a variável independente se aproxima do ponto onde o limite é zero. |
| Gráfico de Barras | As barras do gráfico se tornam cada vez mais estreitas e baixas à medida que a variável independente se aproxima do ponto onde o limite é zero. |
| Gráfico de Dispersão | Os pontos do gráfico se agrupam cada vez mais próximos do eixo x à medida que a variável independente se aproxima do ponto onde o limite é zero. |
| Gráfico de Áreas | A área sob a curva do gráfico se torna cada vez menor à medida que a variável independente se aproxima do ponto onde o limite é zero. |
Cada tipo de gráfico possui suas vantagens e desvantagens para visualizar o limite zero. Por exemplo, o gráfico de linhas é ideal para visualizar o comportamento da função em um intervalo contínuo, enquanto o gráfico de barras é mais adequado para representar dados discretos.
A escolha do tipo de gráfico depende do tipo de dados e do objetivo da visualização.
Exemplos de Gráficos

Vamos considerar a função f(x) = x^2 – 1. O limite de f(x) quando x tende a 1 é zero. Podemos representar essa função graficamente para ilustrar o conceito de limite zero.
Para construir o gráfico, podemos seguir as seguintes etapas:
- Calcular os valores de f(x) para diferentes valores de x. Por exemplo, podemos calcular f(0) =
1, f(1) = 0, f(2) = 3, etc.
- Plotar os pontos (x, f(x)) em um plano cartesiano.
- Traçar uma linha suave que passa pelos pontos plotados.
O gráfico da função f(x) = x^2 – 1 mostra que a função se aproxima de zero à medida que x se aproxima de 1. A linha do gráfico se aproxima do eixo x à medida que x se aproxima de 1, ilustrando o limite zero.
Aplicações do Limite Zero
O conceito de limite zero possui diversas aplicações reais em diferentes áreas do conhecimento. Por exemplo, na física, o limite zero é usado para modelar o movimento de objetos em queda livre. Quando um objeto é solto de uma determinada altura, sua velocidade aumenta gradualmente até atingir uma velocidade terminal.
Essa velocidade terminal é o limite da velocidade do objeto quando o tempo tende ao infinito. Em outras palavras, a velocidade do objeto se aproxima da velocidade terminal à medida que o tempo passa.
Na engenharia, o limite zero é utilizado para modelar o comportamento de sistemas dinâmicos. Por exemplo, em um sistema de controle de temperatura, o limite zero é usado para determinar a temperatura de equilíbrio do sistema. O sistema tende a se estabilizar em uma determinada temperatura à medida que o tempo passa, e essa temperatura de equilíbrio é o limite da temperatura do sistema quando o tempo tende ao infinito.
Na economia, o limite zero é utilizado para modelar o crescimento econômico. Por exemplo, o crescimento econômico de um país pode ser modelado como uma função do tempo. O limite zero nesse caso representa o crescimento econômico de longo prazo.
Em outras palavras, o crescimento econômico de um país tende a se estabilizar em um determinado nível à medida que o tempo passa, e esse nível de crescimento é o limite do crescimento econômico quando o tempo tende ao infinito.

