Análise de um Escoamento Laminar Completamente Desenvolvido: De Boa, Vamos Lá!: Exemplo 5.9 Analise De Um Escoamento Laminar Completamente Desenvolvido
Exemplo 5.9 Analise De Um Escoamento Laminar Completamente Desenvolvido – A gente vai desvendar o mistério do escoamento laminar completamente desenvolvido, tipo, aquele fluxo super suave e previsível. Vamos entender suas características principais, comparar com o caos do escoamento turbulento, e aplicar tudo isso no Exemplo 5.9, de forma que até sua vó vai entender.
Características do Escoamento Laminar Completamente Desenvolvido, Exemplo 5.9 Analise De Um Escoamento Laminar Completamente Desenvolvido
Imagine um rio fluindo suavemente, sem turbulências ou redemoinhos. Esse é o conceito básico. Em um escoamento laminar completamente desenvolvido, as partículas de fluido movem-se em camadas paralelas, sem mistura significativa entre elas. A velocidade do fluido é constante ao longo do tempo em cada ponto, e o perfil de velocidade é bem definido e previsível. A viscosidade do fluido desempenha um papel chave, mantendo as camadas organizadas.
A diferença crucial em relação ao escoamento turbulento é a ausência de redemoinhos e mistura caótica. No escoamento turbulento, a velocidade varia aleatoriamente no tempo e no espaço, resultando em mistura intensa e perda de energia significativa devido ao atrito.
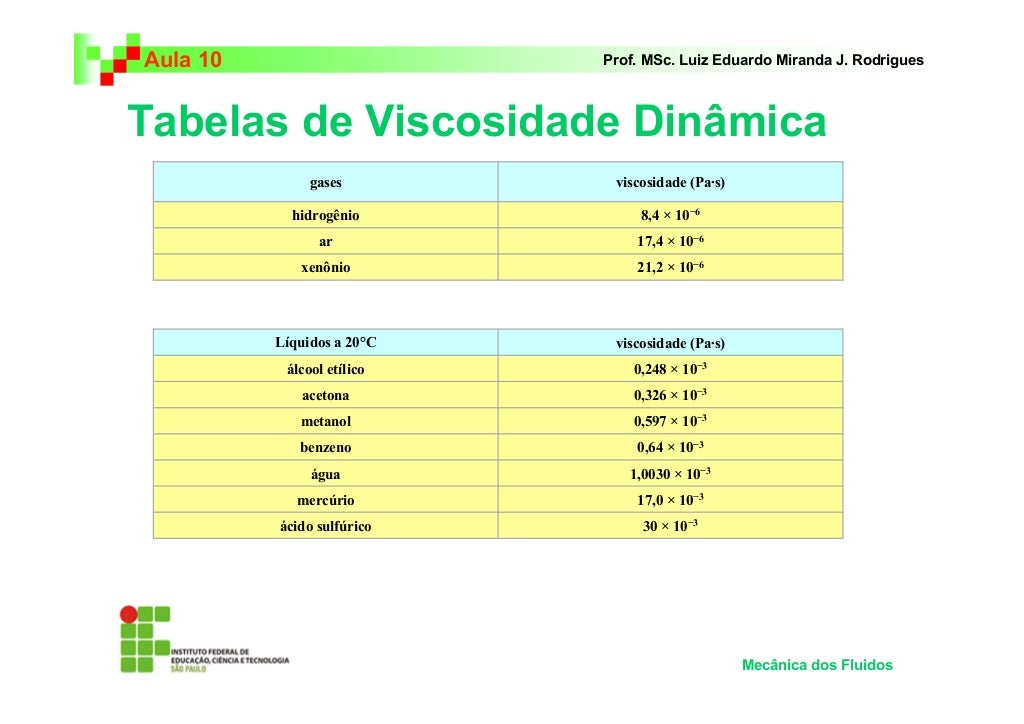
Para simplificar a análise, geralmente assumimos que o fluido é Newtoniano (a tensão de cisalhamento é diretamente proporcional à taxa de deformação), incompressível (densidade constante), e o escoamento é estacionário (não varia com o tempo). Também podemos ignorar efeitos de gravidade em alguns casos.
Equações de Navier-Stokes Simplificadas para o Exemplo 5.9

As equações de Navier-Stokes, que descrevem o movimento de fluidos, são bem complexas. Mas, para o Exemplo 5.9 (assumindo um escoamento laminar entre placas paralelas, por exemplo), elas se simplificam bastante. As condições de contorno são aplicadas nas superfícies das placas, definindo a velocidade do fluido nesses pontos (geralmente zero na parede, devido à condição de não deslizamento). A resolução, em geral, envolve integração das equações simplificadas, considerando as condições de contorno, para obter o perfil de velocidade.
Por exemplo, uma equação simplificada poderia ser: μ(d²u/dy²) = ΔP/L, onde μ é a viscosidade dinâmica, u é a velocidade, y é a coordenada perpendicular à direção do escoamento, ΔP é a diferença de pressão e L é o comprimento do canal.
Perfil de Velocidade e Tensão de Cisalhamento
Resolvendo as equações simplificadas (como a apresentada acima), obtemos um perfil de velocidade parabólico para o escoamento entre placas paralelas. Em um tubo circular, o perfil seria parabólico também, mas com simetria radial. A tensão de cisalhamento, que representa a força interna no fluido devido à viscosidade, é calculada usando a lei de viscosidade de Newton (τ = μ(du/dy)).
| Posição (y) | Velocidade (u) | Tensão de Cisalhamento (τ) | Observações |
|---|---|---|---|
| 0 | 0 | Máxima | Parede |
| y/2 | u_máx/2 | Metade da máxima | Meio do canal |
| y | u_máx | 0 | Centro do canal |
| -y/2 | u_máx/2 | Metade da máxima | Meio do canal |
O gráfico da tensão de cisalhamento seria uma linha reta, começando com um valor máximo na parede e diminuindo linearmente até zero no centro do canal. O gráfico do perfil de velocidade seria uma parábola, com velocidade zero na parede e velocidade máxima no centro.
Vazão e Queda de Pressão
A vazão volumétrica é obtida integrando o perfil de velocidade sobre a área da seção transversal do escoamento. A queda de pressão ao longo de um determinado comprimento é diretamente proporcional à vazão, ao comprimento e à viscosidade do fluido, e inversamente proporcional à área da seção transversal. Fluidos mais viscosos requerem maior queda de pressão para a mesma vazão.
Análise Dimensional e Número de Reynolds
A análise dimensional permite identificar os grupos adimensionais relevantes, como o Número de Reynolds (Re), que é a razão entre as forças de inércia e as forças viscosas. Um Re baixo indica um escoamento laminar, enquanto um Re alto indica um escoamento turbulento. Para o Exemplo 5.9, o cálculo do Re depende dos valores específicos do problema, mas se o valor for menor que 2300 (para escoamento em um tubo circular), o escoamento é considerado laminar.
Aplicações Práticas do Escoamento Laminar Completamente Desenvolvido
Escoamentos laminares completamente desenvolvidos são relevantes em diversas aplicações, como microfluídica (sistemas com canais muito pequenos), lubrificação (camadas finas de fluido entre superfícies em movimento), e processos de fabricação que envolvem o controle preciso do fluxo de fluidos. Em projetos de engenharia, esse conhecimento é crucial para o dimensionamento de dutos, bombas e outros equipamentos que trabalham com fluidos. Escoamentos laminares são geralmente menos eficientes em termos de transporte de fluidos do que escoamentos turbulentos, pois a mistura é mínima, resultando em menores taxas de transferência de calor e massa.
O que acontece se o escoamento parar de ser laminar?
Aí vira turbulento, mano! Tudo fica mais bagunçado, com redemoinhos e perdas de energia.
Quais são as aplicações práticas mais comuns disso?
Em sistemas de refrigeração, microfluídica, e até mesmo no design de alguns tipos de coração artificial, cara.
Existe algum software que simula isso?
Sim, vários! Como o ANSYS Fluent e o OpenFOAM, por exemplo. São bem poderosos.

