De Exemplo De Ponto Reta Segmento De Reta Semireta Plano: Mergulhe no universo da geometria, onde pontos infinitamente pequenos se unem para formar retas que se estendem até o infinito, segmentos que definem limites e semirretas que partem em uma jornada sem fim. Imagine um palco imenso, o plano, onde essas entidades geométricas dançam uma coreografia eterna, traçando relações complexas e revelando a beleza da ordem matemática.
Prepare-se para decifrar os mistérios dessas formas fundamentais, que moldam nosso mundo desde a construção de imponentes edifícios até a complexidade dos circuitos eletrônicos.
Nesta jornada geométrica, exploraremos a definição precisa de cada elemento – ponto, reta, segmento de reta e semirreta – e como eles se inter-relacionam, criando uma estrutura fundamental para a compreensão do espaço. Veremos como o plano, um conjunto infinito de pontos, serve como cenário para as interações entre retas, revelando posições relativas como paralelismo, concorrência e inclusão.
Através de exemplos concretos e ilustrações, desvendaremos as aplicações práticas desses conceitos em diversas áreas do conhecimento, desde a arquitetura e engenharia até o design e a arte.
Conceitos Geométricos Básicos: Uma Visão Balinesa: De Exemplo De Ponto Reta Segmento De Reta Semireta Plano
Hayo, galerinha! Vamos mergulhar no mundo da geometria, mas com aquele toque “Bali vibes”, de boas e sem stress. A gente vai explorar pontos, retas, segmentos, semirretas e planos, coisas que a gente vê todo dia, sem nem perceber! Preparem as cangas e os óculos de sol, que a viagem vai começar!
Conceitos Fundamentais: Ponto, Reta, Segmento e Semirreta
Imagine a praia: a areia, o mar, o céu… tudo cheio de pontos, retas, segmentos e semirretas! Vamos entender melhor cada um deles, com exemplos bem “pé na areia”.
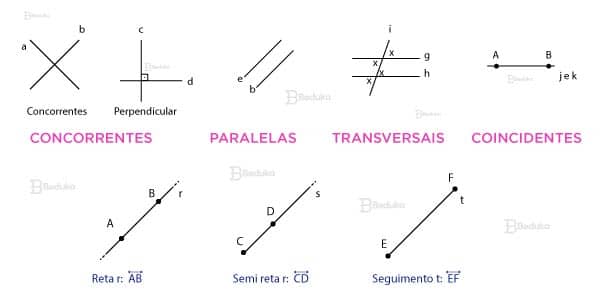
- Ponto: É a menor unidade da geometria, sem dimensão. Pense numa única granulação de areia. Representado por uma letra maiúscula (A, B, C…).
- Reta: Uma sequência infinita de pontos, sem começo nem fim. Imagine a linha do horizonte no mar, que se estende infinitamente. Representada por uma letra minúscula (r, s, t…) ou por dois pontos (AB).
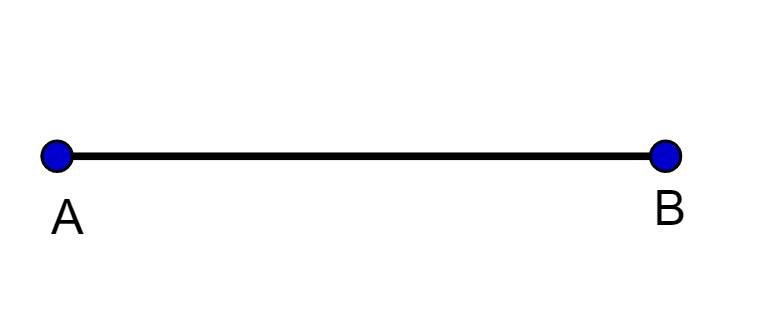
- Segmento de Reta: Uma parte finita de uma reta, com um início e um fim. Pense numa tábua de surfe, com comprimento definido. Representado por dois pontos (AB).
- Semirreta: Uma parte de uma reta que começa em um ponto e se estende infinitamente em uma única direção. Imagine um raio de sol que parte do sol e vai até o fim do universo. Representado por um ponto e uma seta (AB).
| Elemento Geométrico | Definição | Representação | Exemplo Cotidiano |
|---|---|---|---|
| Ponto | Unidade sem dimensão | A | Grão de areia |
| Reta | Sequência infinita de pontos | — | Linha do horizonte |
| Segmento de Reta | Parte finita de uma reta | —– | Tábua de surfe |
| Semirreta | Parte de uma reta com início definido | —–> | Raio de sol |
O Plano como Conjunto de Pontos
Agora, vamos ampliar a visão. O plano é como uma superfície plana e ilimitada, que contém infinitos pontos, retas e outros elementos geométricos. Pense numa grande folha de papel, que se estende infinitamente em todas as direções, ou na superfície da água calma.
- Reta e Plano: Uma reta pode ser paralela a um plano (nunca se encontram), intersectar o plano (se cruzam em um ponto) ou estar contida no plano (toda a reta está sobre o plano).
Exemplos do dia a dia: o chão da sua casa, a parede, a superfície da mesa, tudo isso pode ser considerado um plano.
Posições Relativas entre Retas e Planos

As retas e planos podem se relacionar de várias maneiras, dependendo de suas posições no espaço. Vamos analisar isso com calma, sem pressa.
| Posição Relativa entre Duas Retas | Descrição | Exemplo |
|---|---|---|
| Paralelas | Nunca se cruzam | Duas linhas de trem paralelas |
| Concorrentes | Se cruzam em um único ponto | Duas ruas que se cruzam |
| Coincidentes | São a mesma reta | Duas cópias da mesma linha |
Uma reta em relação a um plano pode ser paralela (nunca se encontram), concorrente (se cruzam em um único ponto) ou contida no plano (está totalmente sobre o plano).
Aplicações Práticas
A geometria, com seus pontos, retas e planos, é fundamental em diversas áreas. Vamos ver alguns exemplos:
- Arquitetura: Na construção de casas, prédios, pontes, etc. Os projetos são baseados em desenhos técnicos que utilizam esses conceitos.
- Engenharia: No planejamento e construção de estradas, ferrovias, etc. A precisão nas medidas é essencial e depende da geometria.
- Desenho Técnico: A representação de objetos tridimensionais em um plano bidimensional utiliza esses conceitos.
Exemplo prático: construir um quadro. Precisamos de pontos para definir os cantos, segmentos de reta para definir as laterais e um plano para a superfície do quadro.
Relações Métricas, De Exemplo De Ponto Reta Segmento De Reta Semireta Plano
Agora, vamos dar uma olhada na matemática por trás da geometria. Vamos falar sobre medidas e relações entre os elementos.
- Comprimento de um Segmento: A distância entre dois pontos. Podemos medir com uma régua.
- Mediatriz de um Segmento: A reta perpendicular ao segmento que passa pelo seu ponto médio.
- Ângulos e Retas Concorrentes: Retas concorrentes formam ângulos. A soma dos ângulos adjacentes é 180 graus.

